Начинающий
- Статус
- Оффлайн
- Регистрация
- 8 Янв 2022
- Сообщения
- 11
- Реакции
- 21
Перевод статьи
Подобной темы на форуме не нашел и решил выкатить перевод.
Думаю, многим будет полезно.
Многие из вас знакомы с печально известным методом "CalcAngle", распространяемым во многих источниках, руководствах и форумах. Я виню в распространении этого метода Fleep'a, который распространил его в одном из своих гайдов. Короче говоря, этот метод довольно плох и имеет некоторые плохие методы программирования, из которых наиболее заметно магическое число 57.2957... Также трудно следить за тем, что происходит на самом деле.
Поэтому вместо того, чтобы копировать этот темный блок кода, я собираюсь научить вас лучшему, быстрому и чрезвычайно точному методу вычисления. Это будет работать как с Internal, так и с External читами, но я настоятельно рекомендую вам попробовать создать Internal чит, так как движок исходного кода игры предоставляет несколько очень полезных вспомогательных функций.
Если вы не знаете, что делает CalcAngle, то он просто принимает две 3D-позиции: src и dst, и выводит угол dst. Это в основном используется в aimbots, где вы вводите положение глаз локального игрока в src, голову цели в dst, а затем устанавливаете углы обзора.
РАЗДЕЛ №1: НЕМНОГО О ВЕКТОРАХ
Вектор - это n-мерный тип данных, в котором хранятся значения декартовых координат. На самом базовом уровне это линия. Наиболее распространенными векторами являются 2- и 3-мерные. 1-мерный вектор обычно называют скаляром и представляют собой просто вещественные числа (т.е. никаких комплексных чисел). Векторы более высокой размерности существуют, но мы не можем представить их на декартовой плоскости, поскольку мы не можем представить их в мировом пространстве.
Вот как выглядит 3-мерный вектор (3,7,5):

Векторы могут быть выражены несколькими способами:
Единичная векторная форма: 3i + 7j + 5k
Это часто используется в математике, но совершенно бесполезно в информатике. i, j и k - это x, y и z соответственно.
Форма упорядоченного набора: (3, 7, 5)
Точно так же, как упорядоченная пара на декартовом графике. Почти все векторы в этом руководстве будут исключительно в этой форме.
Полярная форма: (9,11, 56,71°)
Это самая интересная форма, так как это вектор, представленный не на декартовой плоскости, а на полярной плоскости. Первый член - это величина или гипотенуза, а второй член - угол, который образует вектор. Мы по существу перейдем к этой форме в конце урока.

Поскольку наш вектор технически представляет собой два объединенных треугольника, мы можем применять к нему обычные тригонометрические функции. Возможно, самая важная часть - это найти величину вектора. Как описано ранее, величина - это длина вектора. Есть два способа сделать это.
Мы можем либо использовать тангенс и решить из гипотенузы XY, а затем снова использовать тангенс и решить из величины. Но мы можем сделать это быстрее. Возможно, вы изучили формулу двумерного расстояния на уроке алгебры. Это вытекает из теоремы Пифагора: a ^ 2 + b ^ 2 = c ^ 2.
Мы собираемся использовать 3D-вариант этой формулы, который аналогичен 2D-формуле, но содержит дополнительный член для третьего измерения.
Конечно, поскольку мы имеем дело с векторами, расстояние всегда будет от начала координат. Таким образом, формулу можно еще больше упростить.
Это основы векторов! Возможно, вам потребуется обратиться к этому разделу руководства позже.
РАЗДЕЛ №2: ПРОБЛЕМА
Итак, мы хотим создать aimbot. Как и в случае с CalcAngle, нам нужно определить углы обзора, которые позволят нам целиться прямо в нашего врага.
Первое, что нам нужно сделать, это определить позицию взгляда нашего локального игрока в мире. Это довольно просто. Вам просто нужно получить исходный вектор и добавить его к смещению взгляда. Затем вы должны найти позицию головы противника.
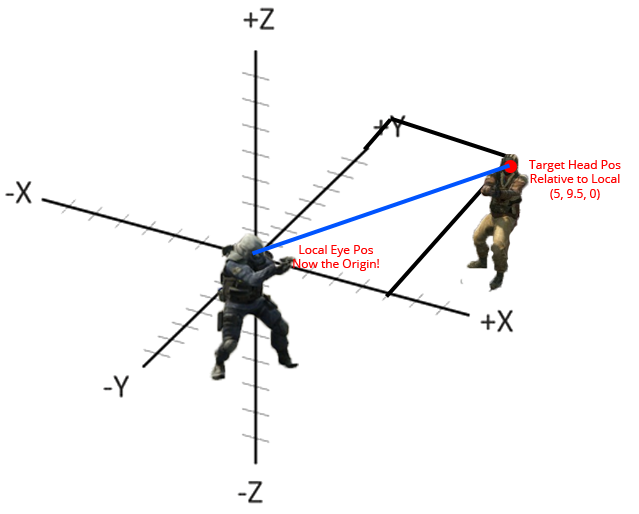
Итак, что нам нужно найти, так это голову цели относительно нашего игрока, по сути, вектор между нами и нашей целью.

Мы можем довольно легко найти этот вектор, вычтя положение наших глаз из положения головы цели. Результирующим вектором будет положение нашей цели относительно нашей головы. Вычитание векторов очень простое. Вы просто вычитаете так, как это было бы с парами чисел.
В нашем примере:
Это результирующий вектор:
РАЗДЕЛ №3: ЗАБАВЫ С ТРИГОНОМЕТРИЕЙ
Отлично! Теперь у нас есть вектор, к которому мы хотим наводиться. Теперь нам просто нужно рассчитать угол, необходимый для наведения на этот вектор.
С этого момента давайте предположим, что углы обзора игрока в примере равны (12°, 30°), что соответствует Pitch и Yaw. Давайте построим углы обзора на полярной координатной плоскости (предположим, что радиус = 1).
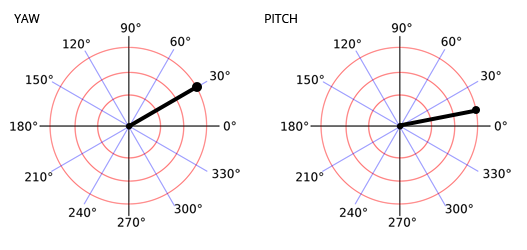
Мы помним, что Pitch - это Y нашего вектора, а Yaw - это X нашего вектора. Как описано в разделе "Немного о векторах" этого руководства, вектор образует прямоугольный треугольник с величиной в качестве гипотенузы. Таким образом, мы можем использовать стандартные тригонометрические функции для нахождения угла.
Величина вектора из нашего примера равна 10,73.
Давайте изобразим вектор на наших окружностях:
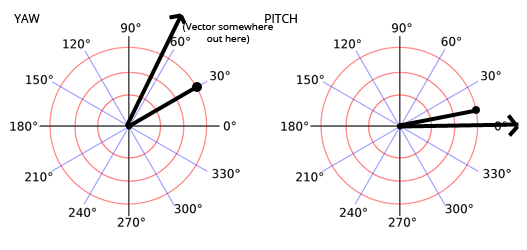
Когда вы визуализируете это таким образом, очень легко увидеть треугольник.
Так что эта проблема очень легко решается.
Помните: гипотенуза - это величина вектора.
РАЗДЕЛ №4: СГЛАЖИВАНИЕ
Если вы хотите сделать rage aimbot или что-то в этом духе, то вы почти закончили! Однако, если вы хотите реализовать плавное прицеливание, это тоже довольно легко. Этот метод мне нравится называть методом сглаживания "нелинейного коэффициента".
Первое, что нам нужно сделать, это вычесть наши вычисленные углы из текущих углов обзора игрока. Как и вычитание вектора, это даст нам угол относительно наших текущих углов обзора, поэтому вы можете просто добавить этот результирующий угол к текущим углам обзора, чтобы получить тот же эффект.
Чтобы сгладить его, просто добавьте результат, разделенный на некоторую константу, к углам обзора.
Например, чтобы сгладить наводку в 4 раза, вы бы использовали:
Я называю это нелинейным, потому что движение мыши становится нелинейным из-за поведения этой функции.
ЗАКЛЮЧЕНИЕ
Пожалуйста, авторизуйтесь для просмотра ссылки.
.Подобной темы на форуме не нашел и решил выкатить перевод.
Думаю, многим будет полезно.
Многие из вас знакомы с печально известным методом "CalcAngle", распространяемым во многих источниках, руководствах и форумах. Я виню в распространении этого метода Fleep'a, который распространил его в одном из своих гайдов. Короче говоря, этот метод довольно плох и имеет некоторые плохие методы программирования, из которых наиболее заметно магическое число 57.2957... Также трудно следить за тем, что происходит на самом деле.
C++:
void CalcAngle( float *src, float *dst, float *angles )
{
double delta[3] = { (src[0]-dst[0]), (src[1]-dst[1]), (src[2]-dst[2]) };
double hyp = sqrt(delta[0]*delta[0] + delta[1]*delta[1]);
angles[0] = (float) (asinf(delta[2]/hyp) * 57.295779513082f);
angles[1] = (float) (atanf(delta[1]/delta[0]) * 57.295779513082f);
angles[2] = 0.0f;
if(delta[0] >= 0.0) { angles[1] += 180.0f; }
}Поэтому вместо того, чтобы копировать этот темный блок кода, я собираюсь научить вас лучшему, быстрому и чрезвычайно точному методу вычисления. Это будет работать как с Internal, так и с External читами, но я настоятельно рекомендую вам попробовать создать Internal чит, так как движок исходного кода игры предоставляет несколько очень полезных вспомогательных функций.
Если вы не знаете, что делает CalcAngle, то он просто принимает две 3D-позиции: src и dst, и выводит угол dst. Это в основном используется в aimbots, где вы вводите положение глаз локального игрока в src, голову цели в dst, а затем устанавливаете углы обзора.
РАЗДЕЛ №1: НЕМНОГО О ВЕКТОРАХ
Вектор - это n-мерный тип данных, в котором хранятся значения декартовых координат. На самом базовом уровне это линия. Наиболее распространенными векторами являются 2- и 3-мерные. 1-мерный вектор обычно называют скаляром и представляют собой просто вещественные числа (т.е. никаких комплексных чисел). Векторы более высокой размерности существуют, но мы не можем представить их на декартовой плоскости, поскольку мы не можем представить их в мировом пространстве.
Вот как выглядит 3-мерный вектор (3,7,5):
Векторы могут быть выражены несколькими способами:
Единичная векторная форма: 3i + 7j + 5k
Это часто используется в математике, но совершенно бесполезно в информатике. i, j и k - это x, y и z соответственно.
Форма упорядоченного набора: (3, 7, 5)
Точно так же, как упорядоченная пара на декартовом графике. Почти все векторы в этом руководстве будут исключительно в этой форме.
Полярная форма: (9,11, 56,71°)
Это самая интересная форма, так как это вектор, представленный не на декартовой плоскости, а на полярной плоскости. Первый член - это величина или гипотенуза, а второй член - угол, который образует вектор. Мы по существу перейдем к этой форме в конце урока.
Поскольку наш вектор технически представляет собой два объединенных треугольника, мы можем применять к нему обычные тригонометрические функции. Возможно, самая важная часть - это найти величину вектора. Как описано ранее, величина - это длина вектора. Есть два способа сделать это.
Мы можем либо использовать тангенс и решить из гипотенузы XY, а затем снова использовать тангенс и решить из величины. Но мы можем сделать это быстрее. Возможно, вы изучили формулу двумерного расстояния на уроке алгебры. Это вытекает из теоремы Пифагора: a ^ 2 + b ^ 2 = c ^ 2.
Мы собираемся использовать 3D-вариант этой формулы, который аналогичен 2D-формуле, но содержит дополнительный член для третьего измерения.
magnitude = sqrt((x2 - x1)^2 + (y2 - y1)^2 + (z2 - z1)^2) // Величина вектораКонечно, поскольку мы имеем дело с векторами, расстояние всегда будет от начала координат. Таким образом, формулу можно еще больше упростить.
magnitude = sqrt(x^2 + y^2 + z^2)Internal users: Исходный SDK предоставляет класс Vector, который инициализируется Vector(x, y, z) и имеет удобную функцию Vector::Length, которая вычисляет величину.
External users: Я предлагаю вам создать структуру, содержащую координаты x, y, z и функцию, которая вычисляет величину вектора.
Это основы векторов! Возможно, вам потребуется обратиться к этому разделу руководства позже.
РАЗДЕЛ №2: ПРОБЛЕМА
Итак, мы хотим создать aimbot. Как и в случае с CalcAngle, нам нужно определить углы обзора, которые позволят нам целиться прямо в нашего врага.
Первое, что нам нужно сделать, это определить позицию взгляда нашего локального игрока в мире. Это довольно просто. Вам просто нужно получить исходный вектор и добавить его к смещению взгляда. Затем вы должны найти позицию головы противника.
Internal users: положение головы противника можно найти с помощью функции IClientEntity::SetupBones, а затем с помощью класса CStudioHdr для получения хитбокса. В интернете есть много руководств о том, как это сделать.
External users: Вам нужно будет повторить структуру костей и найти кость, которая вам нужна. Об этом так же есть много руководств.
Подсказка: Идентификатор кости головы для игроков равен 8.
Итак, что нам нужно найти, так это голову цели относительно нашего игрока, по сути, вектор между нами и нашей целью.
Мы можем довольно легко найти этот вектор, вычтя положение наших глаз из положения головы цели. Результирующим вектором будет положение нашей цели относительно нашей головы. Вычитание векторов очень простое. Вы просто вычитаете так, как это было бы с парами чисел.
В нашем примере:
Код:
( 3 , 4.5 , 5 )
- ( -2 , -5 , 5 )
------------------
( 5 , 9.5 , 0 )Internal users: SDK предоставляет вспомогательную функцию VectorSubtract(a, b, c), где векторами для вычитания являются a и b, а результирующий вектор равен c.
External users: DirectX предоставляет вспомогательную функцию D3DXVec3Subtract(out, a, b).
Это результирующий вектор:

РАЗДЕЛ №3: ЗАБАВЫ С ТРИГОНОМЕТРИЕЙ
Отлично! Теперь у нас есть вектор, к которому мы хотим наводиться. Теперь нам просто нужно рассчитать угол, необходимый для наведения на этот вектор.
С этого момента давайте предположим, что углы обзора игрока в примере равны (12°, 30°), что соответствует Pitch и Yaw. Давайте построим углы обзора на полярной координатной плоскости (предположим, что радиус = 1).

Мы помним, что Pitch - это Y нашего вектора, а Yaw - это X нашего вектора. Как описано в разделе "Немного о векторах" этого руководства, вектор образует прямоугольный треугольник с величиной в качестве гипотенузы. Таким образом, мы можем использовать стандартные тригонометрические функции для нахождения угла.
Величина вектора из нашего примера равна 10,73.
Давайте изобразим вектор на наших окружностях:

Когда вы визуализируете это таким образом, очень легко увидеть треугольник.
У нас есть X и Y, поэтому мы можем использовать arctan, или обратную касательную, чтобы найти yaw.
У нас есть Z и гипотенуза, поэтому мы можем использовать arccos или обратный косинус, чтобы найти pitch.
Так что эта проблема очень легко решается.
yaw = arctan(y/x) // think sin = opp/hyp, cos = adj/hyp, tan = sin/cospitch = arccos(z/hypotenuse)Помните: гипотенуза - это величина вектора.
Internal users: Вы можете использовать функцию SDK VectorAngles(vector, angle), чтобы легко рассчитать pitch и yaw.
РАЗДЕЛ №4: СГЛАЖИВАНИЕ
Если вы хотите сделать rage aimbot или что-то в этом духе, то вы почти закончили! Однако, если вы хотите реализовать плавное прицеливание, это тоже довольно легко. Этот метод мне нравится называть методом сглаживания "нелинейного коэффициента".
Первое, что нам нужно сделать, это вычесть наши вычисленные углы из текущих углов обзора игрока. Как и вычитание вектора, это даст нам угол относительно наших текущих углов обзора, поэтому вы можете просто добавить этот результирующий угол к текущим углам обзора, чтобы получить тот же эффект.
Чтобы сгладить его, просто добавьте результат, разделенный на некоторую константу, к углам обзора.
Например, чтобы сгладить наводку в 4 раза, вы бы использовали:
cmd->viewangles += angleBetween / 4Я называю это нелинейным, потому что движение мыши становится нелинейным из-за поведения этой функции.
ЗАКЛЮЧЕНИЕ
- Найдите вектор цели относительно локального игрока.
- Преобразуйте этот вектор в угол.
- Примените нелинейный коэффициент, если вам нужно сглаживание.
Последнее редактирование:

