- Статус
- Оффлайн
- Регистрация
- 22 Авг 2022
- Сообщения
- 1,248
- Реакции
- 178
Казалось бы, такой простой на первый взгляд модуль, который состоит из кучи строк кода.
AABB и причём здесь коллизия
Axis Aligned Bounding Box (AABB) - в переводе означает параллелепипед оси которого выровнены относительно координат в которых он находится. Чуть позже вы поймёте это, а сейчас просто представьте себе объёмный прямоугольник (параллелепипед).
Для взаимодействия между объектами и их физикой придумали хитбокс. Данный хитбокс имеет форму того самого AABB, скорее всего вы его уже видели много раз:

Пишем
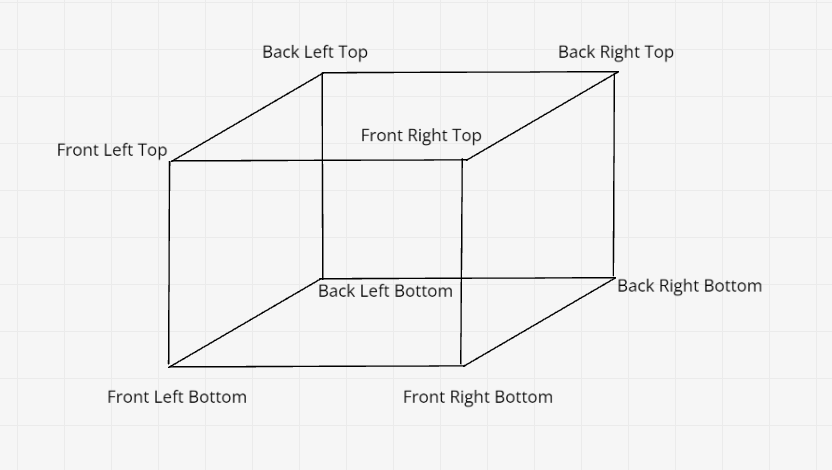
Большинство игр представляют AABB в виде двух точек: минимальную (нижний левый передний угол) и максимальную (верхний правый задний угол). Этого достаточно, чтобы получить все 8 точек параллелепипеда.
Предлагаю создать структуру AABB и выразить в ней те две точки:
Теперь напишем метод получения 8 вершин. Пишем именно в таком порядке, чтобы потом не пересобирать массив векторов для преобразования в 2д прямоугольник (позже я упомяну про него):
Трансформация
Теперь вспомним определение AABB. Это параллелепипед оси которого выровнены относительно координат в которых он находится.
Формально, нам нужно преобразовать каждую вершину к трансформации (позиции и ротации) игрока.
Визуально трансформацию и её значения можно посмотреть в любом (почти) 3д движке игр:
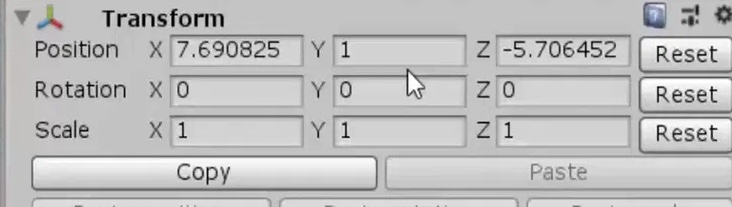
Для трансформации нужно создать две функции, одну для поворота (rotation) и другую для перемещения (translation) матрицы 3 на 4:
Так как для поворота служит кватернион, то матрица для него выбрана такая:
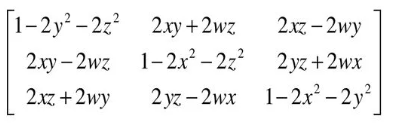
Примечание: В очень редких случаях кватернион может иметь представление в виде:
Теперь, применяем эти матрицы к нашей точке:
Теперь, имея преобразованные и готовые к работе координаты вершин, можно их спроектировать (AKA WorldToScreen) в координаты на экране:
И затем с помощью полученных вершин на экране создать прямоугольник (кстати выше я упоминал про порядок точек, вот здесь он как раз и нужен):
Думаю на этом всё. Если есть люди которые шарят в этом - жду от вас комментариев.
AABB и причём здесь коллизия
Axis Aligned Bounding Box (AABB) - в переводе означает параллелепипед оси которого выровнены относительно координат в которых он находится. Чуть позже вы поймёте это, а сейчас просто представьте себе объёмный прямоугольник (параллелепипед).
Для взаимодействия между объектами и их физикой придумали хитбокс. Данный хитбокс имеет форму того самого AABB, скорее всего вы его уже видели много раз:

Пишем
Большинство игр представляют AABB в виде двух точек: минимальную (нижний левый передний угол) и максимальную (верхний правый задний угол). Этого достаточно, чтобы получить все 8 точек параллелепипеда.
Предлагаю создать структуру AABB и выразить в ней те две точки:
C++:
// да я привык писать длинные, но максимально понятные названия классам и структурам
struct AxisAlignedBoundingBox {
Vector3 min, max;
};Теперь напишем метод получения 8 вершин. Пишем именно в таком порядке, чтобы потом не пересобирать массив векторов для преобразования в 2д прямоугольник (позже я упомяну про него):
C++:
Vector3* GetVertices() const {
Vector3* vertices = new Vector3[8];
Vector3 frontLeftBottom(max.x, min.y, min.z);
Vector3 backRightTop(min.x, max.y, max.z);
Vector3 backLeftBottom(min.x, min.y, min.z);
Vector3 frontRightTop(max.x, max.y, max.z);
Vector3 frontRightBottom(max.x, max.y, min.z);
Vector3 backRightBottom(min.x, max.y, min.z);
Vector3 backLeftTop(min.x, min.y, max.z);
Vector3 frontLeftTop(max.x, min.y, max.z);
vertices[0] = frontLeftBottom;
vertices[1] = backRightTop;
vertices[2] = backLeftBottom;
vertices[3] = frontRightTop;
vertices[4] = frontRightBottom;
vertices[5] = backRightBottom;
vertices[6] = backLeftTop;
vertices[7] = frontLeftTop;
return vertices;
}
Трансформация
Поправьте меня если я неправ с утверждением ниже.
Теперь вспомним определение AABB. Это параллелепипед оси которого выровнены относительно координат в которых он находится.
Формально, нам нужно преобразовать каждую вершину к трансформации (позиции и ротации) игрока.
Визуально трансформацию и её значения можно посмотреть в любом (почти) 3д движке игр:

Для трансформации нужно создать две функции, одну для поворота (rotation) и другую для перемещения (translation) матрицы 3 на 4:
C++:
static void RotateMatrix(Matrix3x4& matrix, const Quaternion& orientation) {
matrix[0][0] = 1.0f - 2.0f * powf(orientation.y, 2) - 2.0f * powf(orientation.z, 2);
matrix[1][0] = 2.0f * orientation.x * orientation.y + 2.0f * orientation.w * orientation.z;
matrix[2][0] = 2.0f * orientation.x * orientation.z - 2.0f * orientation.w * orientation.y;
matrix[0][1] = 2.0f * orientation.x * orientation.y - 2.0f * orientation.w * orientation.z;
matrix[1][1] = 1.0f - 2.0f * powf(orientation.x, 2) - 2.0f * powf(orientation.z, 2);
matrix[2][1] = 2.0f * orientation.y * orientation.z + 2.0f * orientation.w * orientation.x;
matrix[0][2] = 2.0f * orientation.x * orientation.z + 2.0f * orientation.w * orientation.y;
matrix[1][2] = 2.0f * orientation.y * orientation.z - 2.0f * orientation.w * orientation.x;
matrix[2][2] = 1.0f - 2.0f * powf(orientation.x, 2) - 2.0f * powf(orientation.y, 2);
}
static void TranslateMatrix(Matrix3x4& matrix, const Vector3& position) {
matrix[0][3] = position.x;
matrix[1][3] = position.y;
matrix[2][3] = position.z;
}Так как для поворота служит кватернион, то матрица для него выбрана такая:
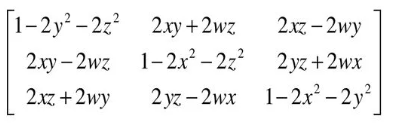
Примечание: В очень редких случаях кватернион может иметь представление в виде:
[U]Vector3 axis, float angle[/U]. Для этого просто конвертируйте его с помощью формулы:
C++:
// Взято со https://stackoverflow.com/questions/12435671/quaternion-lookat-function функция CreateFromAxisAngle
float halfAngle = angle / 2.0f;
float sinHalfAngle = sinf(halfAngle);
float x = axis.x * sinHalfAngle;
float y = axis.y * sinHalfAngle;
float z = axis.z * sinHalfAngle;
float w = cosf(halfAngle);Теперь, применяем эти матрицы к нашей точке:
C++:
Vector3* vertices = aabb.GetVertices();
for (int i = 0; i < 8; i++) {
Vector3& point = vertices[i];
Matrix3x4 matrix{};
Matrix3x4::RotateMatrix(matrix, orientation);
Matrix3x4::TranslateMatrix(matrix, position);
point *= matrix;
}Теперь, имея преобразованные и готовые к работе координаты вершин, можно их спроектировать (AKA WorldToScreen) в координаты на экране:
C++:
Vector2 screenVertices[8];
for (int i = 0; i < 8; i++) {
if (!math::WorldToScreen(viewMatrix, vertices[i], screenVertices[i]))
return INVALID_RECT;
}И затем с помощью полученных вершин на экране создать прямоугольник (кстати выше я упоминал про порядок точек, вот здесь он как раз и нужен):
C++:
Vector2 frontLeftBottom = screenVertices[0];
float left = frontLeftBottom.x;
float top = frontLeftBottom.y;
float right = frontLeftBottom.x;
float bottom = frontLeftBottom.y;
for (int i = 1; i < 8; i++) {
Vector3 vertex = screenVertices[i];
if (left > vertex.x)
left = vertex.x;
if (top < vertex.y)
top = vertex.y;
if (right < vertex.x)
right = vertex.x;
if (bottom > vertex.y)
bottom = vertex.y;
}
Rect rect{};
rect.x = left;
rect.y = bottom;
rect.width = right - left;
rect.height = top - bottom;
return rect;Думаю на этом всё. Если есть люди которые шарят в этом - жду от вас комментариев.

